How to find the LCM of Numbers

Use the worksheets.site password to open the PDF file.

1. What is the Least Common Multiple

A multiple of a number is the product of that number and an integer. For example, 10 is a multiple of 5 because 5 × 2 = 10, so 10 is divisible by 5 and 2. Because 10 is the smallest positive integer that is divisible by both 5 and 2, it is the least common multiple of 5 and 2.

2. Example of finding the LCM the hard way

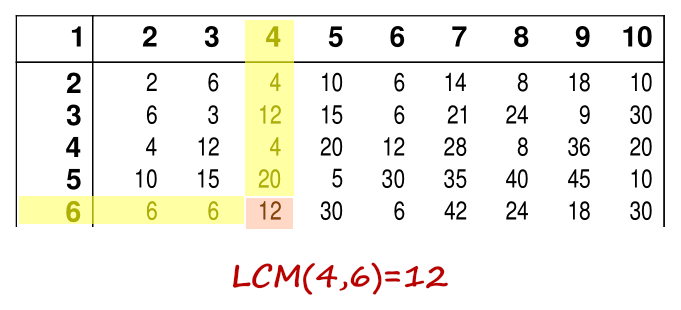
To calculate LCM(4, 6) we can follow this procedure:

Find multiples of 4 are:

Find multiples of 6 are:

Common multiples of 4 and 6 are the numbers that are in both lists:

So, from this list of the first few common multiples of the numbers 4 and 6, their least common multiple is 12. The number 12 is common to both list, hence the name least common multiple.

3. Using the table find the lowest common multiple

By contrast, we can easily find the value of the LCM(4, 6) by looking at the number in the intersection of the corresponding row and column in the table provided . Use the password worksheets.site to open the PDF.

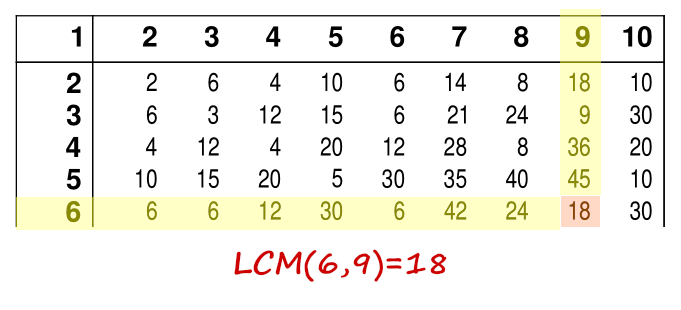
Similarly, and just as easy it is to find the LCM of any pair of numbers below 100, for example LCM(6,9):

4. Application to addition and substration of fractions

When adding, subtracting, or comparing simple fractions, the least common multiple of the denominators often called the lowest common denominator is used because each of the fractions can be expressed as a fraction with this denominator, they are equivalent fractions. For example,

where the denominator 42 was used because it is the least common multiple of 21 and 6.

5. LCM of 3 Numbers

The LCM operation is associative, and that means that the LCM of three numbers A, B and C, is LCM(LCM(A,B),C) and also LCM(A,LCM(B,C)). So find the LCM of any two of the three numbers and then find the LCM of the result and the remaining number. For example:

Similar Worksheets

Math Tables

Home Page