How to find the Number of Combinations
Use the worksheets.site password to open the PDF file.
1. What is a Combination?
A combination is a mathematical concept that describes the number of possible arrangements in a collection of items where the order of the selection does not matter. In combinations, you can select the items in any order. For example, if we have a set of 3 letters {A, B, C}, then the set of arrangements of two letters is AB, BC, AC. That is 3 possible arragements, 3 combinations. Notice that the arragement BA is already considered, it is the same arragement that contains both A and B.
Combinations can be confused with permutations. However, in permutations, the order of the selected items is essential. For example, the arrangements AB and BA are equal in combinations (considered as one arrangement), while in permutations, the arrangements are different.
For example, given three fruits, say an apple, an orange and a pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange.
Combinations are studied in combinatorics but are also used in different disciplines, including mathematics, probability, statistics, finance, computer science.
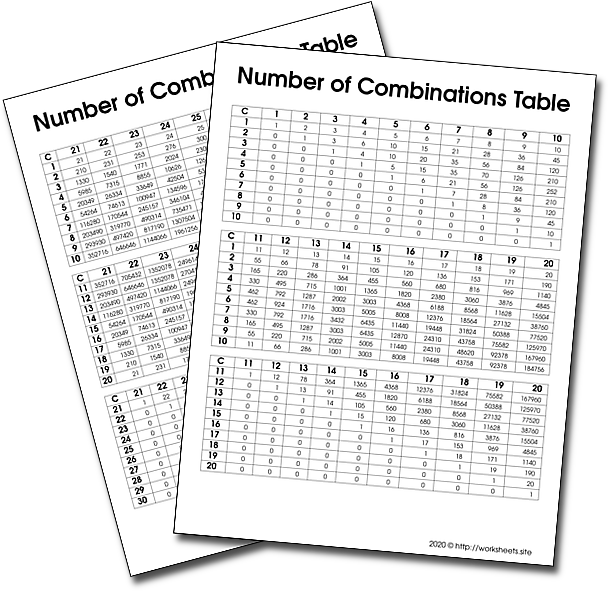
The table of number of combinations ![[PDF Document]](innards/pdf.png)
of two integers will help students calculate the resulting combinations without using the usual mathematical formula.
Combinations refer to the combination of n things taken k at a time without repetition. If, in the above example, it were possible to have two of any one kind of fruit there would be 3 more 2-selections: one with two apples, one with two oranges, and one with two pears.
A table of combinations like this one can be used to make a Pascal's Triangle.
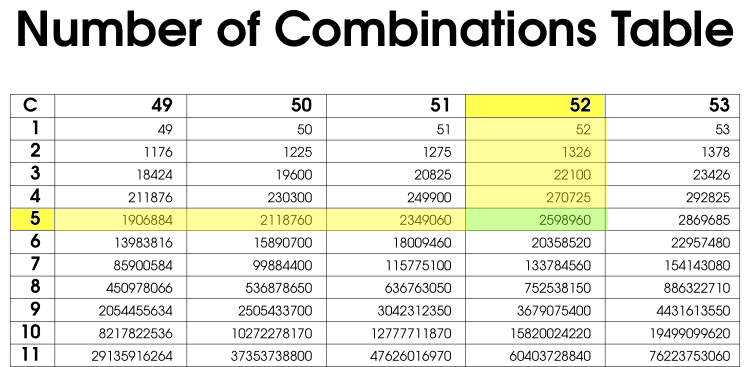
Although the set of three fruits was small enough to write a complete list of combinations, with large sets this becomes impractical. For example, a poker hand can be described as a 5-combination (k = 5) of cards from a 52 card deck (n = 52). The 5 cards of the hand are all distinct, and the order of cards in the hand does not matter. There are 2,598,960 such combinations, and the chance of drawing any one hand at random is 1 / 2,598,960.
The table con be used to find the value in this way:
